Lesson 1.11.1 : R-squared (R²)

R-squared (R²) in Machine Learning

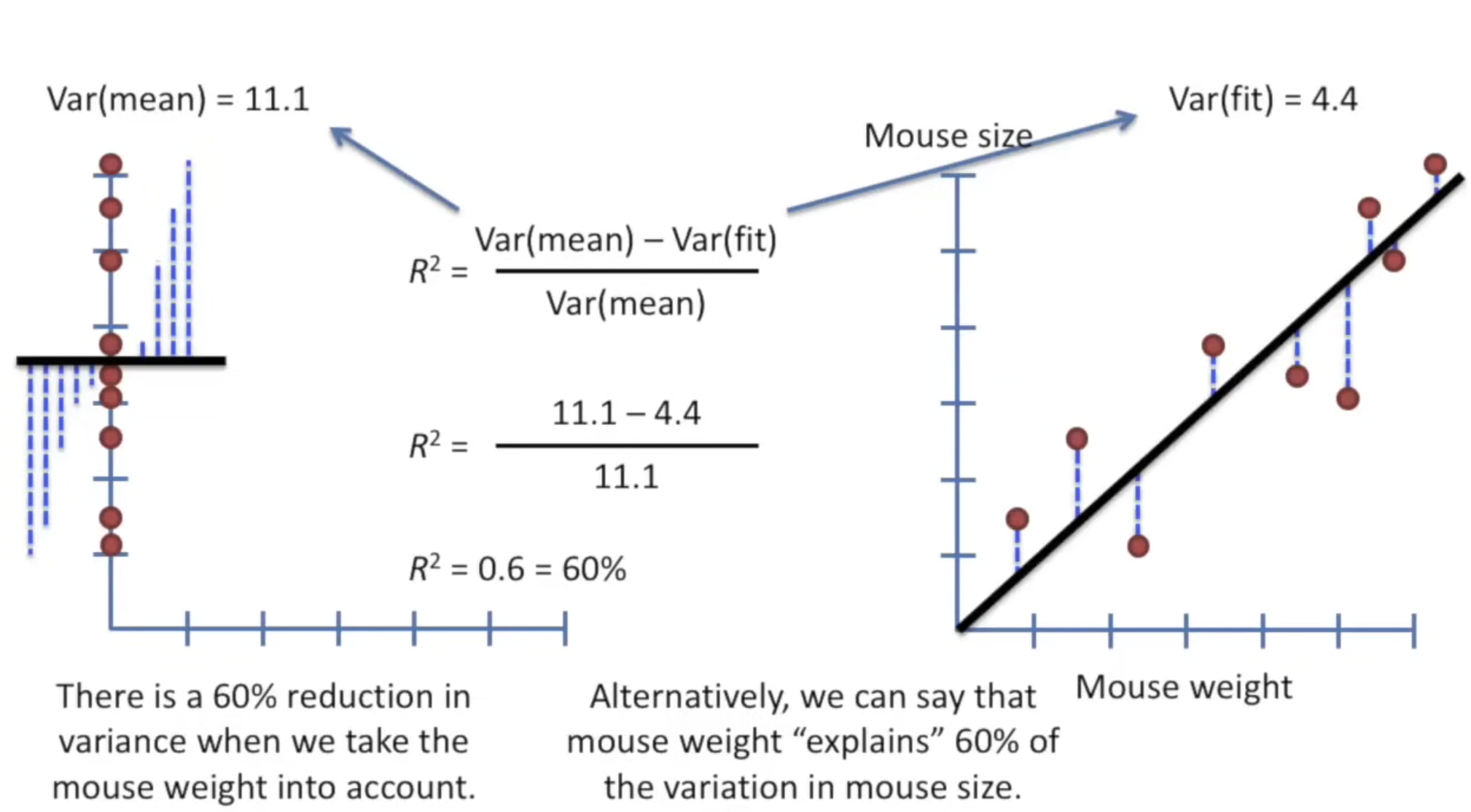
R-squared, also known as the coefficient of determination, is a statistical measure that explains how well a regression model fits the observed data. It indicates the proportion of variance in the dependent variable (target) that is predictable from the independent variables (features).

• Range: 0 to 1 (or 0% to 100%)
• Interpretation:
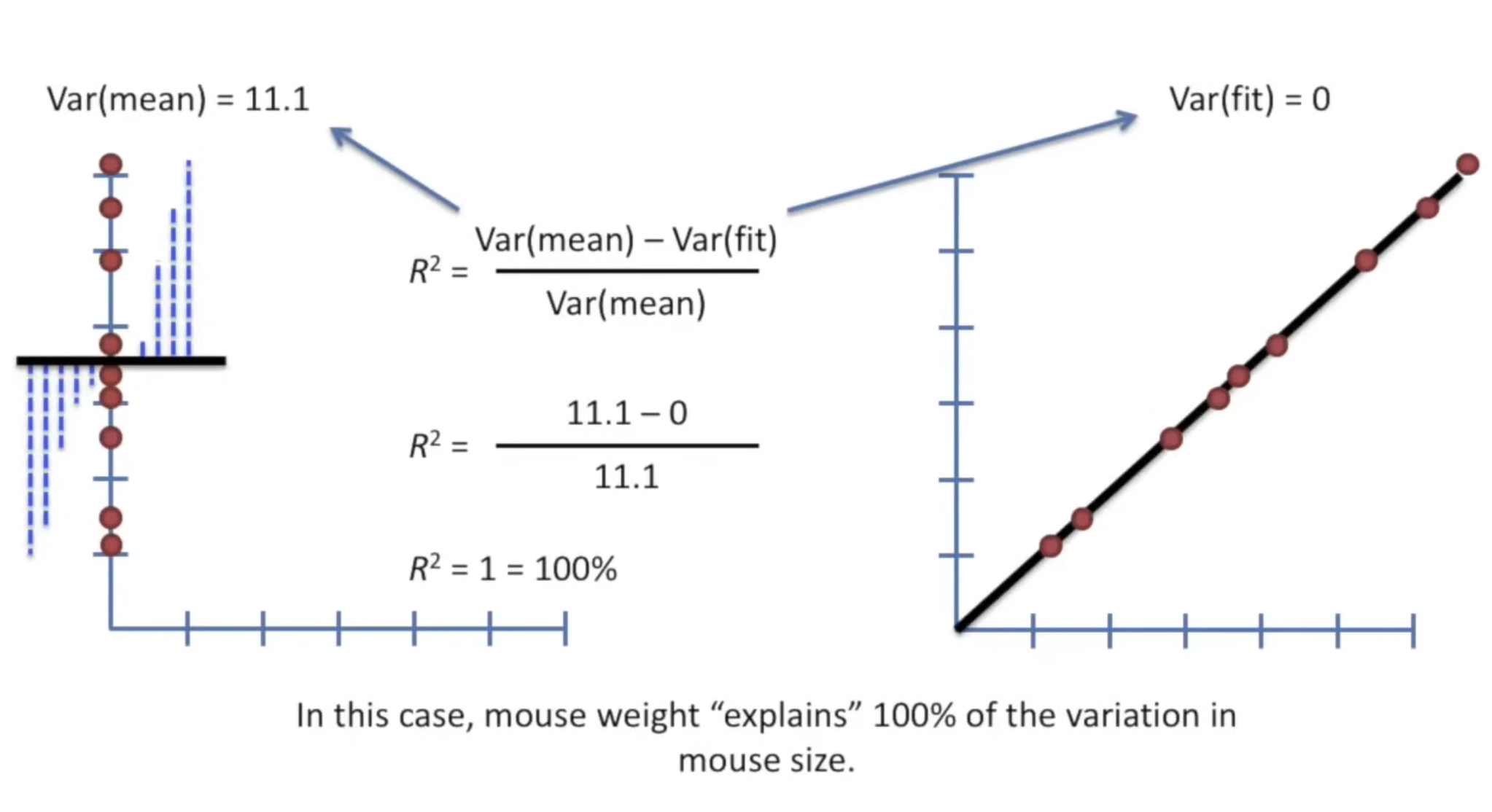
  • R² = 1 → Perfect fit (all data points lie on the regression line).
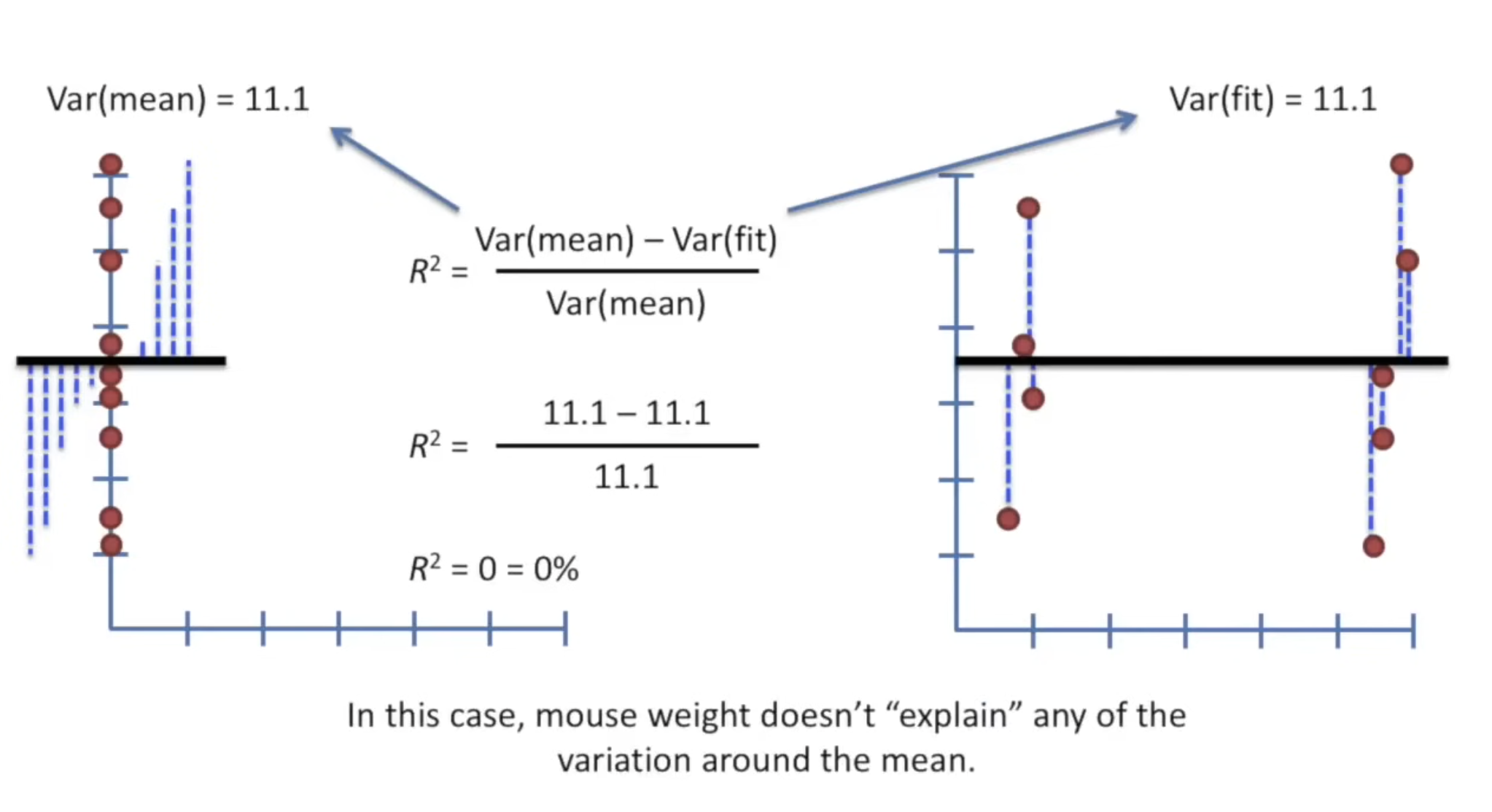
  • R² = 0 → Model explains none of the variability (no better than predicting the mean).
  • Negative R² → Model performs worse than a horizontal line (possible if the model is arbitrarily bad).

R-squared Formula

The coefficient of determination is defined as:

$R^2 = 1 - \frac{\text{SS}_{\text{res}}}{\text{SS}_{\text{tot}}}$ Where:

• SS_res = Sum of squared residuals (errors)
• SS_tot = Total sum of squares (variance in the target)

Example 1: Simple Linear Regression

Data:

Calculations:

1. Mean of $Y$ ($\bar{Y}$):
   $\frac{200k + 250k + 300k + 350k}{4} = 275,000$
2. $\text{SS}_{\text{tot}}$:
   $(200k-275k)^2 + (250k-275k)^2 + (300k-275k)^2 + (350k-275k)^2 = 18.75 \times 10^9$
3. $\text{SS}_{\text{res}}$:
   $(200k-210k)^2 + (250k-240k)^2 + (300k-270k)^2 + (350k-300k)^2 = 4.1 \times 10^9$
4. $R^2$:
   $R^2 = 1 - \frac{4.1 \times 10^9}{18.75 \times 10^9} = 0.781 \quad (\text{78.1\%})$

Interpretation: The model explains 78.1% of the variance in house prices.

Example 2: Perfect Fit ($R^2 = 1$)

Data:

$R^2 = 1 - \frac{0}{\text{SS}_{\text{tot}}} = 1$

Example 3: Poor Fit ($R^2 = 0$)

Data:

$R^2 = 1 - \frac{200}{200} = 0$

Key Notes

• $R^2 = 1$: Perfect fit.
• $R^2 = 0$: Model predicts mean.
• Limitations: Use adjusted $R^2$ for multiple regression.

Key Takeaways:

• When someone says, "The statistically significant $R^2$ was 0.9...", you can think of yourself :
  • Very Good! The relationship between the two variables explains 90% of the variation in data.
• When someone says, "The statistically significant $R^2$ was 0.01..." you can think of yourself :
  • Who Cares! If that relationship is significant, it only accounts for 1% variation in the data.
  • Something else must explain the remaining 99%.